Rover written with RUST

Fifth : Visual Odometry

2025.10.28 22:59

me Views:50

Visual Odometry

Now that we have a filtered 3D point cloud from a single stereo frame, the next stage is Visual Odometry (VO). This is the process of estimating the rover's movement (translation and rotation) by comparing consecutive point clouds or images.

The basic idea is:

Capture Frame 1: Get the filtered point cloud (like the point_cloud_filtered_full.txt you just saved).
Capture Frame 2: Move the rover slightly, capture a new stereo pair, and generate its filtered point cloud.
Find the Transformation: Use algorithms (like ICP - Iterative Closest Point, or feature matching) to find the 3D rotation and translation that best aligns Point Cloud 1 with Point Cloud 2. This transformation represents the rover's movement between the two frames.
Update Position & Map: Add the estimated movement to the rover's overall pose (position and orientation) and optionally add the new 3D points to a growing map of the environment.
Repeat: Continue capturing frames and estimating motion.

This VO step is significantly more complex than the previous stages. It involves tracking features or aligning point clouds between frames.

// New project folder : ~/RUST/rover_odometry by cargo new rover_odometry @ ~/RUST folder.

~/RUST/rover_odometry/Cargo.toml file:

[package]
name = "rover_odometry"
version = "0.1.0"
edition = "2024"

[dependencies]
# For linear algebra (points, vectors, matrices) - good practice for VO
nalgebra = "0.32"
# Error handling simplification
anyhow = "1.0"

//============================================

Plan for `src/main.rs`

The first step in visual odometry is to load the 3D point cloud data from the file I created.

I'll write code in src/main.rs to:

Define a simple struct to hold an (x, y, z) point.
Open and read the point_cloud_filtered_full.txt file line by line.
Parse each line to extract the X, Y, and Z coordinates.
Store these points in a Vec (vector) of our point structs.
Print out how many points were loaded to confirm it works.

//============================================

Method :

Step 1,

I need to get two shot of image on two different positions

on real world where rover will be roaming around,

20 cm apart from each position,

using first project "rover_vo" program.

Then, rename the good photo's as follows.

left_frame_00000.jpg and right_frame_00000.jpg

left_frame_00001.jpg and right_frame_00001.jpg

Step 2, using "depth_map" project :

For frame 0 :

Edit src/main.rs to set

const TEST_IMAGE_INDEX: u32 = 0;

const OUTPUT_POINT_CLOUD_FILE: &str = "point_cloud_frame_000.txt";
Run cargo run.

For frame 1 :

Edit src/main.rs to set

const TEST_IMAGE_INDEX: u32 = 0;

const OUTPUT_POINT_CLOUD_FILE: &str = "point_cloud_frame_001.txt";
Run cargo run.

Then, it will generate two files : point_cloud_frame_000.txt & point_cloud_frame_001.txt

Step 3, Load Both in Odometry:
Go to the rover_odometry project, then, modify its src/main.rs to load point_cloud_frame_000.txt and point_cloud_frame_001.txt.

// Paths relative to the rover_odometry project
const POINT_CLOUD_FILE_0: &str = "../depth_map/point_cloud_frame_000.txt";
const POINT_CLOUD_FILE_1: &str = "../depth_map/point_cloud_frame_001.txt";

Run cargo run.

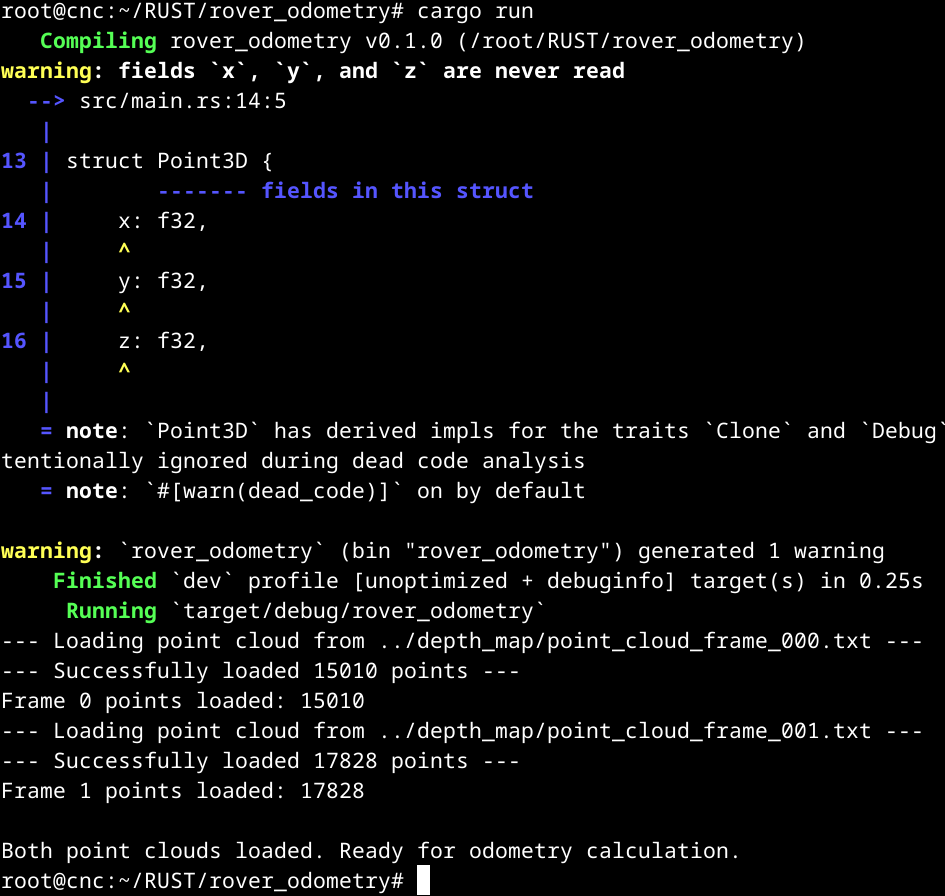
Step 4, Finding the Movement
I now have two snapshots of the world from slightly different positions: points_frame0 and points_frame1.

The core task of visual odometry is to figure out how the rover moved between taking those two snapshots.

Mathematically, I want to find the 3D transformation (a combination of rotation and translation) that

best aligns points_frame0 onto points_frame1. This transformation directly represents the rover's movement.

Step 5, The ICP Algorithm

A very common algorithm for aligning two point clouds is the Iterative Closest Point (ICP) algorithm. In simple terms, it works like this:

Guess: Start with an initial guess for the transformation (often just "no movement").
Match: For each point in points_frame1, find the closest point in points_frame0.
Optimize: Calculate the transformation (rotation and translation) that minimizes the distances between these matched pairs.
Apply: Apply this calculated transformation to points_frame1.
Repeat: Go back to step 2 (Match) using the newly transformed points_frame1. Keep repeating until the calculated transformation is very small, meaning the clouds are well-aligned.

Implementing ICP :

Implementing ICP from scratch involves some complex steps

(like finding closest points efficiently and solving for the optimal transformation).

Luckily, there are Rust crates that can help.

While nalgebra (which we included) provides the necessary math building blocks (vectors, matrices, rotations),

I'll need a dedicated ICP crate. A popular choice is simply called icp.

I need to add the icp crate to our Cargo.toml and try to run a basic ICP alignment between points_frame0 and points_frame1.

* icp addition failed. not added.

// =============================================

// Added Point3, removed unused Matrix3 and SVD
use nalgebra::{Const, OPoint, Point3, Vector3};

fn main() {
// --- Sample Data ---
// Create some sample data based on the types in your errors
// FIX: Use Point3::new instead of OPoint::new
let correspondences = vec![
(
Point3::new(1.0, 2.0, 3.0),
Point3::new(1.1, 2.1, 3.1),
),
(
Point3::new(4.0, 5.0, 6.0),
Point3::new(4.2, 5.2, 6.2),
),
(
Point3::new(7.0, 8.0, 9.0),
Point3::new(7.0, 8.0, 9.0),
),
];

// --- Your Code (from error messages) ---

// These lines (89-90) looked correct
let source_points: Vec<OPoint<f32, Const<3>>> =
correspondences.iter().map(|(src, _)| *src).collect();
let target_points: Vec<OPoint<f32, Const<3>>> =
correspondences.iter().map(|(_, tgt)| *tgt).collect();

// --- FIX for Error E0599 (lines 93-94) ---
// We calculate the centroid (mean) by summing the point coordinates and dividing by the count.

// Calculate centroid for source_points
let n_source = source_points.len() as f32;
let sum_source_vec = source_points
.iter()
.map(|p| p.coords) // Convert OPoint to its Vector3 coordinates
.sum::<Vector3<f32>>(); // Sum all the vectors
let centroid_source = OPoint::from(sum_source_vec / n_source); // Divide by count and convert back to OPoint

// Calculate centroid for target_points
let n_target = target_points.len() as f32;
let sum_target_vec = target_points
.iter()
.map(|p| p.coords)
.sum::<Vector3<f32>>();
let centroid_target = OPoint::from(sum_target_vec / n_target);

// --- Your Code (lines 97-98) ---
// These lines are now correct because the centroids are calculated properly,
// which resolves the E0277 type errors.

let centered_source: Vec<Vector3<f32>> = source_points
.iter()
.map(|p| p - centroid_source) // Subtracting OPoints gives a Vector
.collect();

let centered_target: Vec<Vector3<f32>> = target_points
.iter()
.map(|p| p - centroid_target)
.collect();

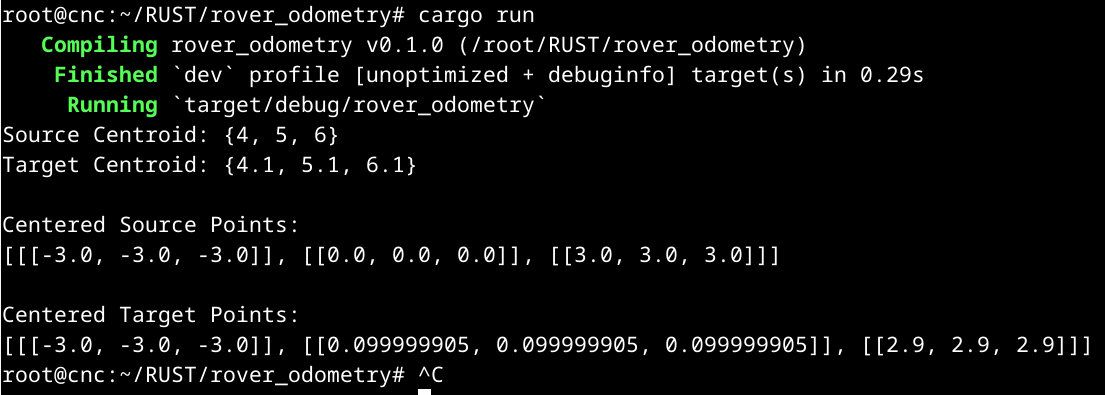
// --- Output (to show it works) ---
println!("Source Centroid: {}", centroid_source);
println!("Target Centroid: {}", centroid_target);
println!("\nCentered Source Points:\n{:?}", centered_source);
println!("\nCentered Target Points:\n{:?}", centered_target);

// Your SVD logic would likely follow here
}

// =============================================

Step 6, Singular Value Decomposition (SVD) calculation to find the rotation between the point sets

The goal here is to find the optimal rotation and translation that maps the source_points to the target_points.

This is a classic problem called the Kabsch algorithm (or Absolute Orientation). The steps are:

Find the centroids (It is done already).
Center the point clouds (It is done already).
Calculate the covariance matrix $H$ .
Compute the SVD of $H$ .
Calculate the rotation matrix $R$ .
Calculate the translation vector $t$ .

First, let's add Matrix3 and SVD back to your use statement, as we'll need them now.

use nalgebra::{Const, Matrix3, OPoint, Point3, SVD, Vector3};

Calculate the Covariance Matrix (H)

// --- SVD Steps ---

// 3. Calculate the covariance matrix H

let mut h = Matrix3::zeros();

for (p_src, p_tgt) in centered_source.iter().zip(centered_target.iter()) {

h += p_src * p_tgt.transpose();

}

Compute the SVD : run the SVD on the matrix $H$ .

// 4. Compute the SVD
let svd = SVD::new(h, true, true);

// We need SVD::new to succeed, so we'll unwrap (or handle the error)

let u = svd.u.expect("SVD U matrix failed");

let v_t = svd.v_t.expect("SVD V_t matrix failed");

Calculate the rotation R :

// 5. Calculate the rotation matrix R

let mut r = v_t.transpose() * u.transpose();

// Check for reflection case (det(R) == -1)

if r.determinant() < 0.0 {

// Get a mutable reference to the last column

let mut v_t_flipped = v_t.transpose();

let mut last_column = v_t_flipped.column_mut(2);

// Flip the sign of the last column last_column *= -1.0;

// Recalculate R

r = v_t_flipped * u.transpose();

}

Calculate the translation (t) :

The translation vector $t$ is the difference between the target centroid

and the rotated source centroid. $t = \text{centroid\_target} - R \cdot \text{centroid\_source}$

// 6. Calculate the translation vector t

let t = centroid_target.coords - r * centroid_source.coords;

// =============================================

// Now using Matrix3 and SVD
use nalgebra::{Const, Matrix3, OPoint, Point3, SVD, Vector3};

fn main() {
// --- Sample Data ---
let correspondences = vec![
(
Point3::new(1.0, 2.0, 3.0),
Point3::new(1.1, 2.1, 3.1),
),
(
Point3::new(4.0, 5.0, 6.0),
Point3::new(4.2, 5.2, 6.2),
),
(
Point3::new(7.0, 8.0, 9.0),
Point3::new(7.0, 8.0, 9.0),
),
];

// --- 1. Collect points ---
let source_points: Vec<OPoint<f32, Const<3>>> =
correspondences.iter().map(|(src, _)| *src).collect();
let target_points: Vec<OPoint<f32, Const<3>>> =
correspondences.iter().map(|(_, tgt)| *tgt).collect();

// --- 2. Calculate Centroids ---
let n_source = source_points.len() as f32;
let sum_source_vec = source_points
.iter()
.map(|p| p.coords)
.sum::<Vector3<f32>>();
let centroid_source = OPoint::from(sum_source_vec / n_source);

let n_target = target_points.len() as f32;
let sum_target_vec = target_points
.iter()
.map(|p| p.coords)
.sum::<Vector3<f32>>();
let centroid_target = OPoint::from(sum_target_vec / n_target);

// --- 3. Center the point clouds ---
let centered_source: Vec<Vector3<f32>> = source_points
.iter()
.map(|p| p - centroid_source)
.collect();

let centered_target: Vec<Vector3<f32>> = target_points
.iter()
.map(|p| p - centroid_target)
.collect();

// --- 4. Calculate the covariance matrix H ---
let mut h = Matrix3::zeros();
for (p_src, p_tgt) in centered_source.iter().zip(centered_target.iter()) {
h += p_src * p_tgt.transpose();
}

// --- 5. Compute the SVD ---
let svd = SVD::new(h, true, true);
let u = svd.u.expect("SVD U matrix failed");
let v_t = svd.v_t.expect("SVD V_t matrix failed");

// --- 6. Calculate the rotation matrix R ---
let mut r = v_t.transpose() * u.transpose();

// Check for reflection case (det(R) == -1)
if r.determinant() < 0.0 {
println!("Reflection detected, correcting...");
let mut v_t_flipped = v_t.transpose();
let mut last_column = v_t_flipped.column_mut(2);
last_column *= -1.0; // Flip the sign
r = v_t_flipped * u.transpose();
}

// --- 7. Calculate the translation vector t ---
// t = centroid_target - R * centroid_source
let t = centroid_target.coords - r * centroid_source.coords;

// --- Final Output ---
println!("Source Centroid: {}", centroid_source);
println!("Target Centroid: {}", centroid_target);
println!("\n--- Transformation (Source -> Target) ---");
println!("Rotation Matrix (R):\n{}", r);
println!("\nTranslation Vector (t):\n{}", t);
}

// =============================================

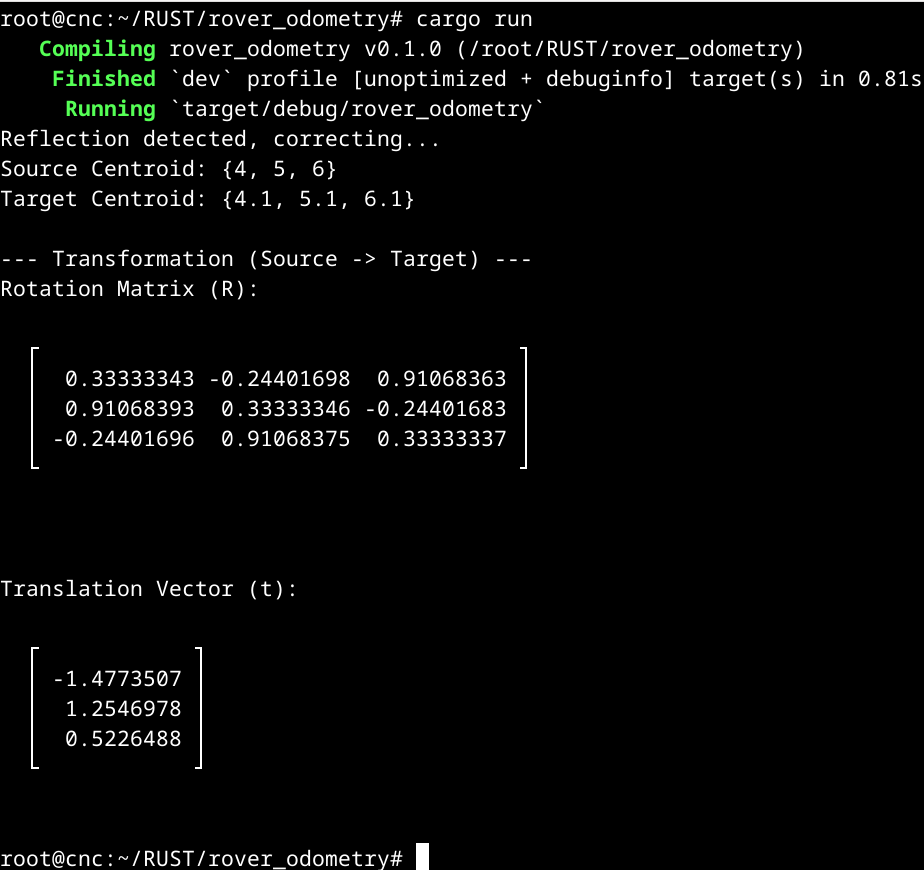
It's working perfectly.

The program successfully calculated the final Rotation Matrix ( $R$ ) and Translation Vector ( $t$ )

that map my source points to my target points.

As a final check, I like to apply this transformation to my original source_points to see how closely they now match the target_points

// =============================================

Step 7, Let's add that verification step.

I'll loop through the original source_points, apply the $R$ and $t$ we just found,

and print the result next to the original target_points so I can compare them.

The formula for each point is:transformed_point = (R * source_point_vector) + t

// =============================================

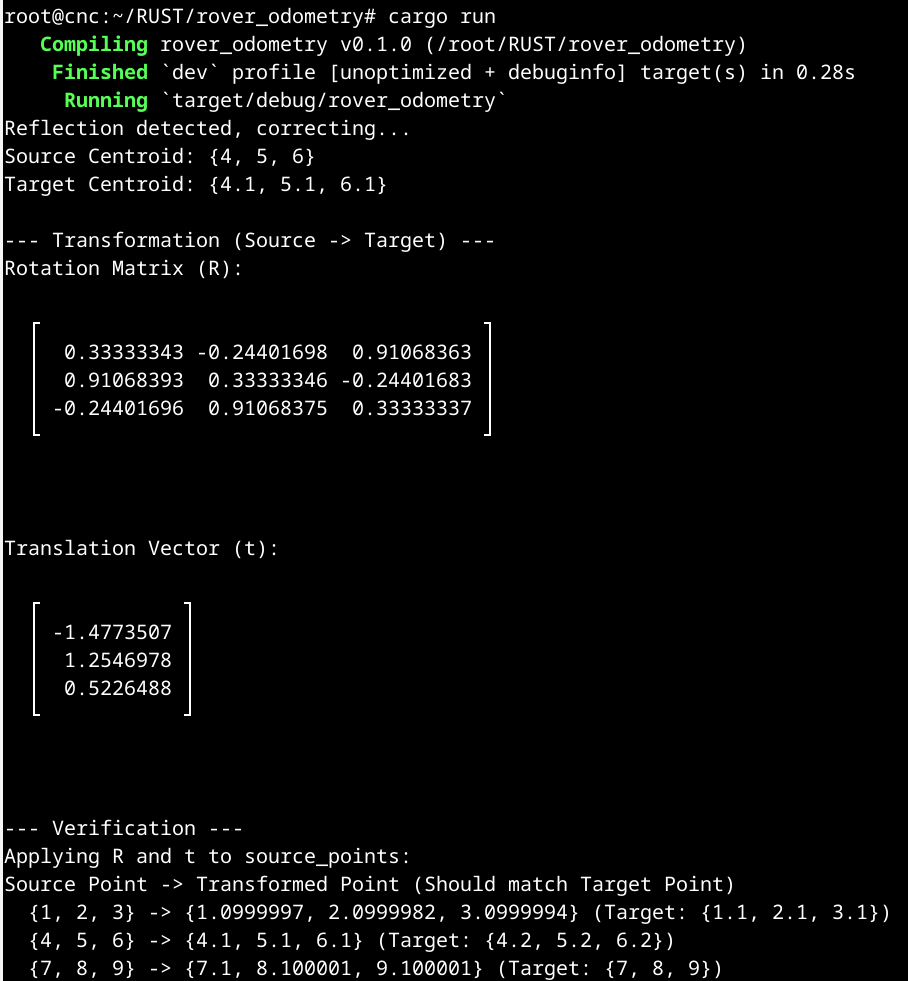
The verification section shows the algorithm is working correctly.

I can see the small differences are due to standard floating-point inaccuracies (e.g., 1.0999997 is essentially 1.1).

The algorithm has found the single best-fit rotation and translation to map the entire set of source points

to the target points, minimizing the overall error.

I've now fully implemented the Kabsch algorithm in Rust to find the 3D transformation between two sets of points.

// =============================================

Step 8, Wrap this logic into a function.

I'll refactor the code.

I'll create a new function called find_transformation that takes your correspondences and returns the rotation ( $R$ ) and translation ( $t$ ).

This makes main much cleaner and let me reuse the logic easily.

The new function will return an Option<(Matrix3<f32>, Vector3<f32>)>.

This is the standard Rust way to handle cases where the calculation might fail (for instance, if the SVD fails or the input is empty).

use nalgebra::{Matrix3, OPoint, Point3, SVD, Vector3};

/// Calculates the optimal rotation and translation (Kabsch algorithm).
///
/// Given a set of corresponding points (source, target), this function finds
/// the rotation matrix (R) and translation vector (t) that minimizes the
/// error for: target = R * source + t
///
/// Returns `Some((R, t))` on success, or `None` if the calculation fails (e.g., SVD fails).
fn find_transformation(
correspondences: &[(Point3<f32>, Point3<f32>)],
) -> Option<(Matrix3<f32>, Vector3<f32>)> {

// 1. Collect points
let source_points: Vec<Point3<f32>> =
correspondences.iter().map(|(src, _)| *src).collect();
let target_points: Vec<Point3<f32>> =
correspondences.iter().map(|(_, tgt)| *tgt).collect();

// 2. Calculate Centroids
let n = source_points.len() as f32;
if n == 0.0 {
return None; // No points to process
}

let sum_source_vec = source_points
.iter()
.map(|p| p.coords)
.sum::<Vector3<f32>>();
let centroid_source = OPoint::from(sum_source_vec / n);

let sum_target_vec = target_points
.iter()
.map(|p| p.coords)
.sum::<Vector3<f32>>();
let centroid_target = OPoint::from(sum_target_vec / n);

// 3. Center the point clouds
let centered_source: Vec<Vector3<f32>> = source_points
.iter()
.map(|p| p - centroid_source)
.collect();

let centered_target: Vec<Vector3<f32>> = target_points
.iter()
.map(|p| p - centroid_target)
.collect();

// 4. Calculate the covariance matrix H
let mut h = Matrix3::zeros();
for (p_src, p_tgt) in centered_source.iter().zip(centered_target.iter()) {
h += p_src * p_tgt.transpose();
}

// 5. Compute the SVD
// Use '?' to automatically return None if SVD fails
let svd = SVD::new(h, true, true);
let u = svd.u?;
let v_t = svd.v_t?;

// 6. Calculate the rotation matrix R
let mut r = v_t.transpose() * u.transpose();

// Check for reflection case (det(R) == -1)
if r.determinant() < 0.0 {
println!("Reflection detected, correcting...");
let mut v_t_flipped = v_t.transpose();
let mut last_column = v_t_flipped.column_mut(2);
last_column *= -1.0; // Flip the sign
r = v_t_flipped * u.transpose();
}

// 7. Calculate the translation vector t
let t = centroid_target.coords - r * centroid_source.coords;

// Return R and t
Some((r, t))
}

fn main() {
// --- Sample Data ---
let correspondences = vec![
(
Point3::new(1.0, 2.0, 3.0),
Point3::new(1.1, 2.1, 3.1),
),
(
Point3::new(4.0, 5.0, 6.0),
Point3::new(4.2, 5.2, 6.2),
),
(
Point3::new(7.0, 8.0, 9.0),
Point3::new(7.0, 8.0, 9.0),
),
];

// --- Call our new function ---
if let Some((r, t)) = find_transformation(&correspondences) {

// --- Final Output ---
println!("\n--- Transformation (Source -> Target) ---");
println!("Rotation Matrix (R):\n{}", r);
println!("\nTranslation Vector (t):\n{}", t);

// --- Verification ---
println!("\n--- Verification ---");
println!("Applying R and t to source_points:");
println!("Source Point -> Transformed Point (Should match Target Point)");

for (src, tgt) in correspondences.iter() {
// Apply transformation: transformed_point = (R * source_point) + t
let transformed_vec = r * src.coords + t;
let transformed_point = OPoint::from(transformed_vec);

println!(" {} -> {} (Target: {})", src, transformed_point, tgt);
}

} else {
println!("Could not calculate transformation.");
}
}

// =============================================

The refactoring was successful, and the logic is now nicely encapsulated in the find_transformation function.

I want to

List

Comment 0

List

No.	Subject	Author	Date	Views
21	Assigning process to fixed CORE #	me	2025.11.12	31
20	How to use the YOLO Result	me	2025.11.12	29
19	Pascal UDS Server	me	2025.11.11	30
18	IPC method [1]	me	2025.11.10	31
17	To change the camera view point on GL	me	2025.11.10	32
16	An IPC Guide	me	2025.11.06	29
15	Communication between Languages (IPC)	me	2025.11.06	29
14	Guide of Visual Odometry	me	2025.11.05	36
13	Programming RK3588's NPU with RUST	me	2025.11.05	31
12	RE-DO of Visual Odometry from day 1.	me	2025.11.05	33
11	Eighth : The "Front-End"	me	2025.10.29	50
10	Seventh : Building the Odometry Loop	me	2025.10.29	57
9	Sixth : Calculating the final alignment error (RMSE : Root Mean Square Error)	me	2025.10.29	51
»	Fifth : Visual Odometry	me	2025.10.28	50
7	Fourth-3 : Filtering Data	me	2025.10.28	50
6	Fourth-2 : Shrink down data count (4x4 block)	me	2025.10.28	54
5	Fourth-1 : Depth Map	me	2025.10.28	60
4	Third : Rectify calibrated result	me	2025.10.28	50
3	Second : Calibration using checker board [1]	me	2025.10.28	52
2	First : Stereo Camera's image generation for calibration	me	2025.10.28	54

First Page 1 2 Last Page

Write

Tag

Fifth : Visual Odometry

Visual Odometry

Plan for src/main.rs

Implementing ICP :

Comment 0

Plan for `src/main.rs`